For a cup of coffee more

First bullet point: There is an interesting analysis of the secret deals that led to the war in Ukraine at the moment by the New York Times, as well as an account of the Trump administration involvement.

This post is brought to you by the letter A for anger issues, and the failed attempt to find an HDMI cable. Why is it that usually there are enough of them to choke two species into extinction, rid Paris of her rat-issues and still have enough for the Praelatura Sanctae Crucis et Operis Dei to flagellate themselves biweekly, but now I cannot find a single one.

Second: Something is rotten in the state of Denmark. Ok, I am being overdramatic; though if I was talking about the level of paranoia this country sometimes presents when faced with youth whose skin is not piggy-pink, that could well be appropriate.

I am also not referring to royal family affairs and the queen’s dental care.

Also, the issue is not really restricted to Denmark. I just really wanted to quote Marcellus.

What I am referring to is an increasing effort to make university a school. And as someone who hated school, let me say:

This comes in the form of a flattening of the study plan, and symptoms include ideas such as

• An overregulation of the study plan
• Turning lectures into Vorlesungen (regurgitation of written material)
• bureaucratic rules preventing individual choice and, I would argue
• grade inflation.

Now, let me first say that I am talking about later years of study; let us for argument’s sake refer to the second year onwards. I agree that a baseline of knowledge is necessary and should be taught. Also, the discussion here applies less to courses of study that are vocational (such as medicine).

Let me also say that grades are, in my point of view, pointless at a university. Noone needs them. Pass fail is where it is at.

For me, the point of university is not preparation for a job; it is a pursuit of interests and inclinations and ideas. That is, at least in most fields. However, as the current drive is towards churning out a specific number of graduates each year (no doubt a politically desirable goal for the statistics), even later semesters become regularized to the extend that

• students have little choice until much later to choose their field of interest, and
• even if they have interests, they are usually prevented by a strict schedule and requirements to actually follow those inclinations.

This later point annoyed me especially, as it essentially prevented students from taking more advanced courses if they had the desire to, which I think can only be described as idiotic. It is then also natural that lectures themselves become stiffer, and a grade inflation takes place (as the hard requirements must be standardized, and the standard cannot be too low.) I am not in principle against the last point, to be clear, but it is ridiculous when, for instance, oral exams are essentially only giving the best, or the best two grades. It is like those eyeroll inducing rating systems in a TV show or game where every value is insanely high and a multiple of 1000. Remove the zeroes, guys.

The result is that the students are surrendered to whatever whim the central authority finds desirable at the moment, and more importantly learn little in the way of independence and, you know, what actually interests them. Not that they know what interests them. Hence, and I know how old I sound, graduate students ask to give the list of proofs they should be able to vomit up on command, rather than understanding the idea of the proof. More grave, many students end up feeling confined to their specializations (which again experience standardization that would make overly anal bureaucrats blush) that, to them, are the only way to survive as a scientist. Plus, as professor actually get to think about making a course interesting, finding another perspective or approach. Dissemination of knowledge can be genius, so why not treat our students to more interesting storytelling, and allow ourselves that flexibility and excitement as well.

And the most important issue may be that within science, you never know what technique leads to which insight. You can take an idea from architecture and translate it to a PDE and then use it to construct interesting polytopes. Interesting ways of thinking get snuffed early, and it is boring. Allowing students to follow their passions of the beaten path can lead to beautiful results, so they should be encouraged to follow their interests freely and I will be excited to see the results. Study classics and physics, for all I care. It is a flattening of skills that is most disheartening.

Speaking of flattening, let me discuss a geometry fact that I am sure is folklore and was most certainly known to Bing.

Thanks to Grigori Avramidi and my friend Eran Nevo for asking me to explain this; thanks also to Geva Yashfe for reminding me by giving a more elegant proof that I leave for him to divulge in an upcoming paper.

The issue is this: say you have a PL embedding of a simplicial complex into a PL manifold M. The question arises: can I think of this as a combinatorial situation? That is, can I find a triangulation T of M such that S is a subcomplex of T? The answer is yes, but with a caveat in that we might have to isotopically change our embedding for this to work (meaning there are situations where it has to be none, and that it is not a shortcoming of the construction), but that is a price we can pay gladly.

The issue is, first of all, that the map may be just wild, that is, facewise not flat: there are faces F of S of codimension dimension k in M such that f cannot be extended to a PL embedding from into M, where denotes the k-dimensional disk.

In other words, facewise there may be points p, for instance in the interior of a maximal face of S, such that the in a neighborhood of f(p), the map is knotted within M.

Note that this notion is distinct from local flatness, a condition sometimes demanded if a manifold N of codimension k embeds into M by demanding that we can extend this to an embedding for a system of open U covering N. In general, it is not possible to make an embedding of manifolds locally flat. We do not have this issue, because while our embedding is supposed to be locally flat in maximal faces, it is not restricted at all at vertices where the embedding can be as wild as we want (as long as it is PL).

Our facewise nonflatness can be remedied by contracting that point away from the interior of that cell, and into a lowerdimensional face of S. Hence we obtain an embedding that is facewise flat in our sense.

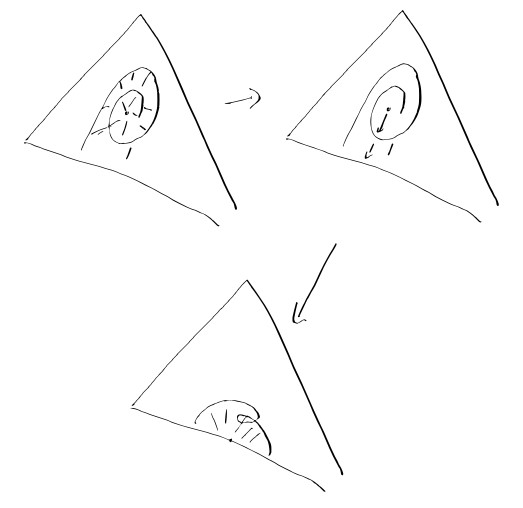
The rest of the argument is due to R. H. Bing, legal name Ronly Honly Bing. Once this facewise flatness is reached, one can, by reverse order on dimension thicken the embedding by shielding it off with simplices. Theorem I.2.A in The Geometric Topology of 3-Manifolds gives the proof for 3-manifolds once the facewise flatness condition is reached (or rather, facewise flatness is automatic in this case).

And that is it. I have given up the search for the HDMI cable. In other current news:

Fluggaenkoecchicebolsen

Edit: changed locally flat to facewise flat to distinguish it from the manifold immersion version.