A useful idea to study an object is, it turns out, not to just consider the object but an entire space of objects like it. Consider, for instance, the situation in which you want to simplify an object to one you understand (like in the solution of the Poincaré conjecture) or when the space is naturally evolving over time (like spacetime): in this case, it is often easier to understand the space of spaces, rather than the space itself, as difficulties like singularities can vanish once you have taken a broader, bird’s eye view.
I want to discuss a specific case of this, based on a great talk Daria Poliakova gave in our seminar. If you don’t like it, well…
The object in question we start with are associativity rules. You know, you have a product abcd, and you ask yourself which one to compute first. You could compute ab, then abc, then abcd. This corresponds to the bracketing ((ab)c)d.
Or you compute bc, then bcd, then abcd. This corresponds to bracketing a((bc)d).
Or you can refuse all this and think about the space of all bracketings directly. You do not only have to consider the finest bracketings (how many brackets are there in any finest bracketing?), but can even consider coarser ones. You can even relate them, by saying that certain brackets are coarser than others. For instance, (ab)cd is coarser than both (ab)(cd) and ((ab)c)d. With this, you are now able to write down a big ancestral tree, called the Hasse diagram, of all of these bracketings.
Dasha prefers to think of this as particles on a line, and recording cascades of collisions. She reported on ongoing work with my former postdoc Spencer Backman and Nate Bottman It is important to notice that she does not record the order of collisions, but just considers the endresult (you can watch the talk in our channel or click here).
In the end, this looks as follows:
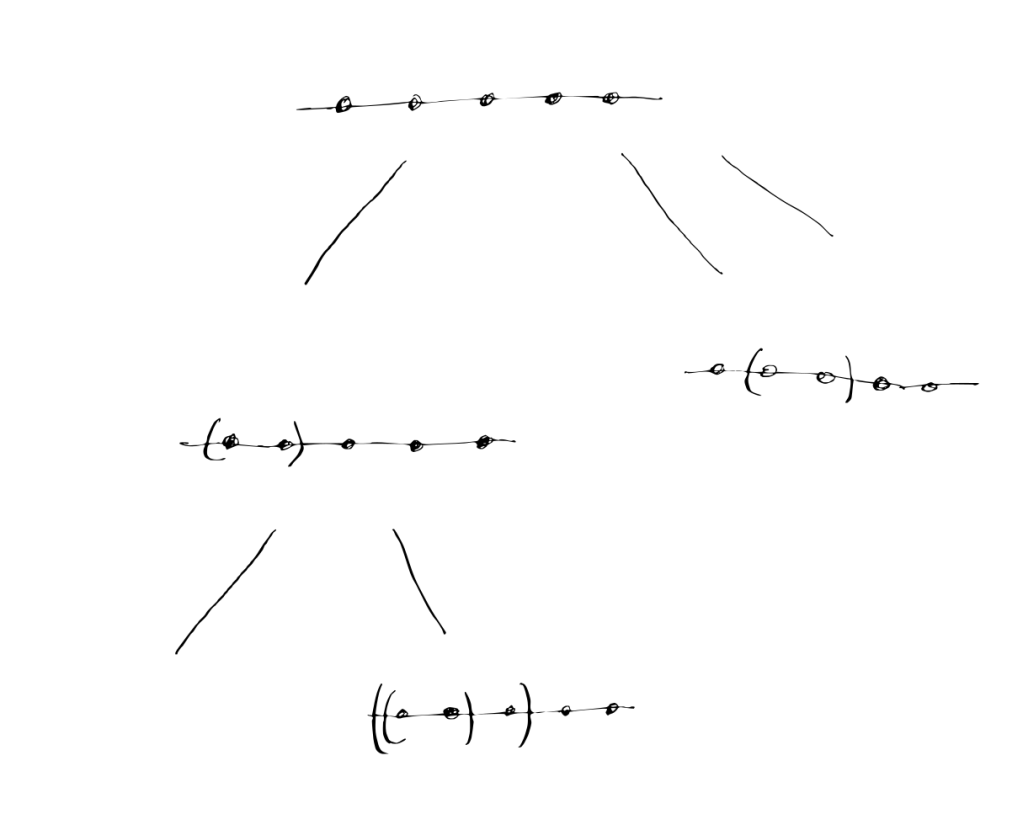
Now, there is a miracle. This space of bracketings itself is a geometric object, called the associahedron. It sits in space as a polytope. And this is not only a novelty: once you understand the geometry of such an object, you can use that geometry, for instance to understand how distant two different bracketings can be. This is of tremendous practical and theoretical use!
There is another way to think of associahedra, and that is via diagonals: Consider a polygon, and draw in diagonals that do not cross. Again, one can order this by looking at coarser sets of diagonals, and finer ones.
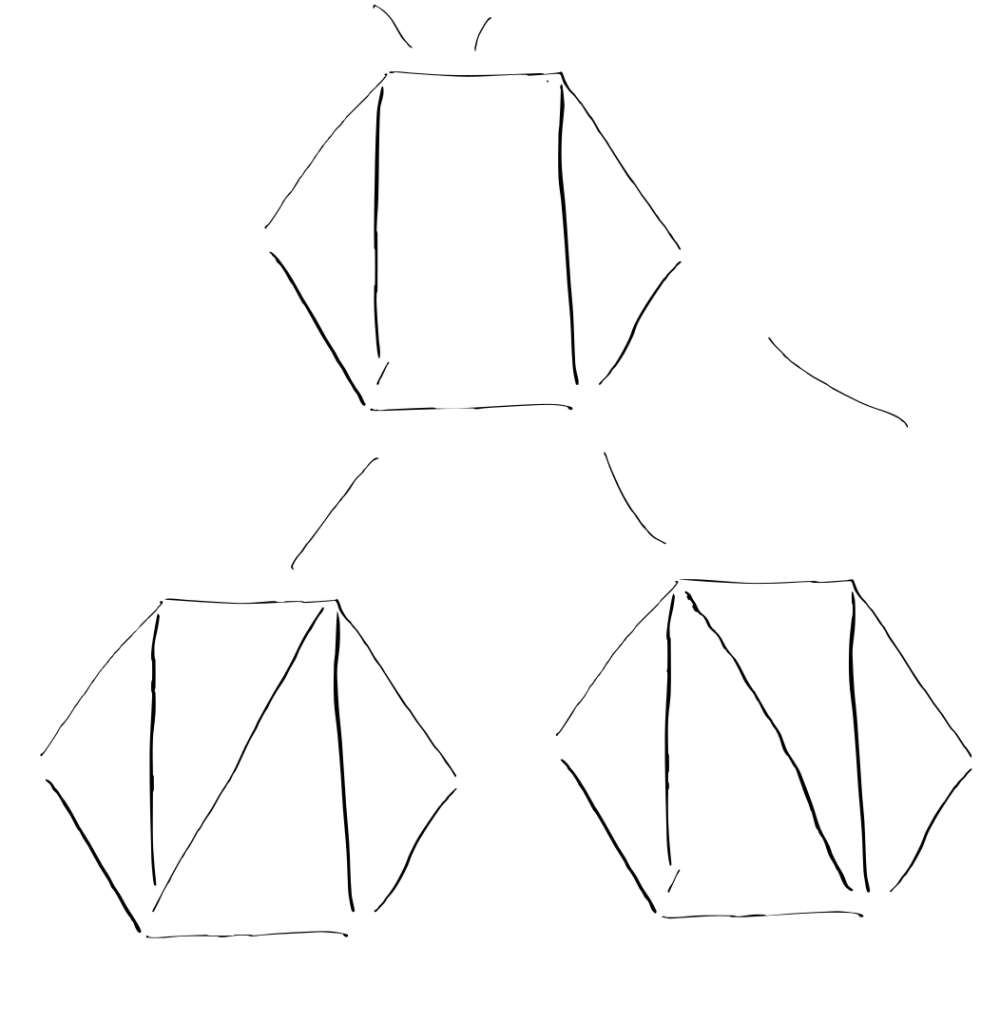
Once again, this leads to a big space, which is another way of thinking about the associahedron (think about the diagonals as dividing the different numbers you want to multiply). And that is all good and fine.
But modern mathematics does not just think about objects and spaces of objects. It thinks about spaces of spaces of objects as well (if you want the technical term, the bracketing philosphy talks about 
Dasha encoded this as follows: instead of having just particles that can collide, there are different spaces as well, and they can collide.
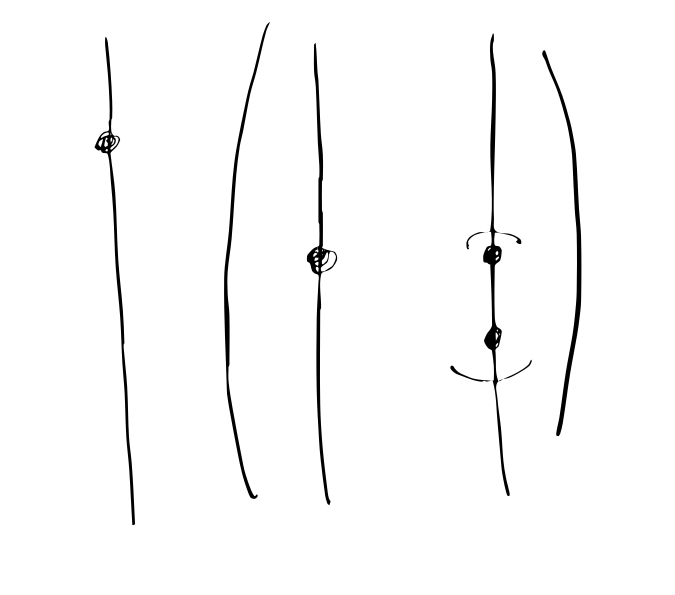
The spaces of these were introduced by Nate Bottman, and Dasha, Spencer and Nate are trying to realize them as polytopes, and she reported on their ongoing efforts.
To make things more confusing, there is another kind of higher associahedra introduced by Vasilis Capoyleas and János Pach. These study the case when diagonals are allowed to cross, but no triple of diagonals is allowed to cross pairwise. Again, the question is whether the resulting space has a geometric realization as polytope. And in parallel to Dasha, Spencer and Nate, they try to understand those realizations.
Of course, one can go even higher than two. It would be interesting to know whether infinity-categories, as important in quantum field theory and higher category theory, could play a simplifying role in the study of these objects.
Thanks Dasha for discussing math and world politics late-night with me. And thank you for Kimchi and mushrooms!
For a cup of coffee more 