Author: Karim Adiprasito

Shhhh. Secrets, entropy and dyslexia

Karim Adiprasito1 Comment
Lefty got something to show and tell you

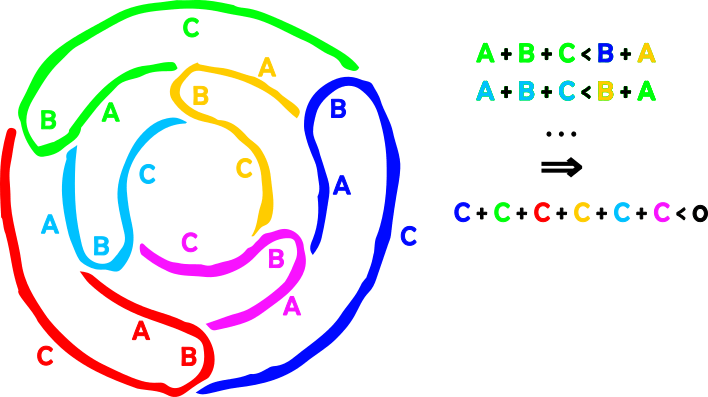
So, say you have some secrets you desperately want to air, but not so desperately that everyone should know. And you are also a little weird, so you only want them to be able to know if they get together and work out the clues. (Oh dear, it sounds like an exhausting gamenight).

Then you have a secret sharing scheme. Specifically, you got yourself into a situation where you have a set P of people, a set C of subsets of P (lets call them conspirators) and a collection of secrets S and Hints H. What you want to do is for a set of people to figure out the information if it contains one of the c in C. Think of it like that Simpsons episode where every single Flying Hellfish was needed to assemble treasure; or think of a more realistic example of a company or agency in which vital information is only accessible by a group. That sort of thing.

Continue reading →

Heart issues, cats and Richard Stanley (unrelated)

Karim AdiprasitoLeave a comment

Since there were some questions as to what happened to the cat this blog is so proudly presenting in its sidebar: He died of a congenital heart defect (a flaw cat and catdad share) that we discovered too late. So I spent two weeks in summer trying to keep his lungs to fill with fluid until I had to free him of his pain.

ridiculously attractive misha
catdad playing catdoctor
His name was Misha, and he made it to age 6.

On a lighter note, Richard Stanley gave an interview and mentioned me solving one of his favorite problems. Yay!

Misha’s gravestone, designed by my sister Ira Adiprasito

Inside Man, shitty chess and exp(anxiety)

Karim AdiprasitoLeave a comment
This image has an empty alt attribute; its file name is stanley-tucci-inside-man-1663777468.jpg
Just look how they butchered my boy

I was watching the new series “Inside Man”, or trying to without jumping off the nearest building, and I came to three conclusions:

  1. Moffat should never be allowed to create more than the pilot of a show. He has a (very) cool idea to start with, but the rest of the show has to bend around increasingly unlikely nonsense to make his plot work to the conclusion he wants to reach.
  2. Kustin-Miller unprojection is cool, and every commutative algebraist should know it; it gives us a way to normalize the seemingly arbitrary. Thank you Stavros for telling me about it. This just because my head drifted off to greener pastures.
  3. People love shitty chess. And they really should not.

Now, let me explain, or rather put up a disclaimer first: By shitty chess, I do not mean the entire Carlsen-Niemann affair. Though perhaps a larger meta-point surrounding deductive (that which is strictly logical) versus inductive reasoning (that is, a game of probabilities) could be made.

Because the reason characters like Sherlock Holmes are so alluring, and the reason we fall for the trap that is Moffat’s skills of giving us a convincing plot, is that we are collectively obsessed with the myth of having everything under control. And perhaps herein lies the issue: when our reasoning invariably fails, we invariably turn to panic and wild plot devices like little men in the derrière. And it is one of the reasons we are collectively anxious all the time (except those that are anyway half in the grave; byebye at this point.)

Continue reading →

Corruption, Lobbyism and postdoc/student positions

Karim AdiprasitoLeave a comment

A while ago, I learned about a case quite curious. Someone offended a foolish little devil, or a devil playing the fool; something small, irrelevant and mosquitolike, the offender a nyaff and nudnik, a gunnif, really. The offender a public person, as it turned out. A politician, if mind serves me well. The story continued to give background to what had been read in newspapers so often; how, determined, files were obtained to prove corruption and bribery. The files were forwarded to authorities, arrests were made. End story.

Reading this, I am not in principle opposed to those acts; to gain favor can be considered parts of human nature. Confusion just arises as to the what and how. And here I intend to be a little helpful. Now, while I am not currently looking for submarines or have critical infrastructure to sell to foreign dignitaries, there have nevertheless been attempts to bribe me for the little I have to offer. For the readers perusal, I will rate some of the bribery attempts that came in material form; though in reality, I am mostly a sucker for what your mind has to offer.

And currently, I am hiring. My research interests you find in the other posts of this blog and my website, but to be honest, I am almost looking to hear something cool. So hit me up and let’s chat.

If you cannot offer ideas, the following might help (heavy sarcasm, because this is the internet). No particular order.

A (mostly) live lizard

A most transparent attempt to gain my favor by my esteemed coauthor. Nevertheless effective. RIP little fucker. I give it a perfect 5/7 lizard tails.

Continue reading →

Convex sets can run, but cannot hide. Also, Parseval-Rayleigh identities in characteristic two and Lefschetz properties for monoid algebras.

Karim AdiprasitoLeave a comment

Let me start with some overdue news, finally released after passive aggressive messages and open bullying. And England’s prime minister got usurped by lettuce. I promise I will start making more sense now.

Erdős and Szekeres famously showed that every set of general position points in the plane contains a large subset of points that is in convex position. And quite recently Andrew Suk improved this so much, that by now we have an essentially tight bound on how many points we can find in convex position, at least in the plane. This was improved a little furtherby Holmsen, Mojarrad, Pach and Tardos here.

But some found that all too plain, and pointed out that in higher dimensions, convex sets could have an even harder time hiding, and that there could be substantially larger convex sets in higher dimensional pointclouds. Alas, noone could prove this until recently, when my friend Cosmin provided, in joint work with Dmitrii Zakharov the first substantial improvement in dimension 3. Congratulations Dima and Cosmin (and see you soon, looking forward to a wintery northeast).

Dmitry Zakharov and Cosmin Pohoaţă in New York

Secondly, our (announcement) preprint on the unimodality of the h*-polynomial is finally online. One curious discovery in this research is that there is a Parseval-Raleigh type identity (Lemma 5.2) for the degree map of the Chow ring associated to the monoid.

Seen as a rational function.

In characteristic two.

In dependence on the torus action/the linear system of parameters.

This really remains to be understood, and we have no clue where it comes from. No phenomenon like that seems to be explored, and we suspect some deep connections to residue theory.

Two coauthors (who unlike others had the decency to stand in alphabetical order) and a dog during a recent joint trip to Cortona, Italy: Stavros Argyrios Papadakis and Vasiliki Petrotou

Art, friends and aesthetically pleasing counterexamples

Karim AdiprasitoLeave a comment

A while ago, Janos Pach told me a question of Peter Maga originating in topological graph theory: Given an arrangement of curves in the plane, can they be realized as geodesics? Due to my Nikolai Mnev‘s universality theorem (and earlier work by Ringel), it is badly impossible to linearize them (stretch them to line segments), even if we assume that any two curves intersect at most once and at that point transversally, that is, if they form a system of pseudo-segments. However, Janos “just” wanted each curve to be a shortest path.

Artwork by Herbert Busemann
Janos Pach (by János Szántó)
Николай Мнёв
3 pictures that lie on more than 3 common lines


This had been proven if the segments extend to infinity by Herbert Busemann (who, as I found out, was also an accomplished artist) and so Janos asked whether it was true in general; this of course would be much more reasonable than the realization along lines (note that the space of all metric spaces with given geodesics would be a disk, rather than the arbitrarily nasty deformation space that Kolya proved whe have when looking for arrangements of real lines.)

So, now we want each line to be the shortest, no two points along it should have shortcut somewhere else. A reasonable request; having dabbled in city planning (read: I played Cities: Skylines like, twice) I imagine it must be the worst nightmare of every real estate developer if the carefully named street is not actually used because a detour using other streets is shorter. (Edit: Conferred with a friend who does spatial planning for a German metropolis. It is not something that keeps him up at night. As with all of us, it is depression and anxieties that keep us up and night. And the decision to have coffee in the evening.)

Jokes aside, this can have real applications, as knowing which routes are shortest (geometer speak: knowing the geodesics and shortest paths) makes planning a route considerably easier (CS speak: faster to compute).

Alas, it turns out to be wrong, and Janos and I found that there are examples where the carefully named and arranged streets are not the shortest. And the aesthetically pleasing example you see here:

It is not hard to see that we cannot give a length metric to this graph such that each of the colored lines is a shortest path; here is the calculation:

And as streets should not have negative length, we are out of luck.

Disclaimer: updates to the post were sponsored by an anonymous professor at Rényi Institute

Anisotropy in arbitrary characteristic, Lefschetz beyond positivity, moment curves and lattice polytopes (part 2)

Karim Adiprasito1 Comment

Just a quick post that kills some questions from the previous post, and a report on just an overall wonderful REU project summer.

So let me start by the following: myself, and then Papadakis and Petrotou, and then us three jointly, proved the Lefschetz property for triangulated spheres (characteristic two in the case of Papadakis and Petrotou). This may be an unfamiliar word for someone not from algebraic geometry, but essentially, it is a property stating that Poincaré duality in certain manifolds coming from algebraic geometry (for instance, smooth projective varieties) is realized in a concrete way. Now you may think combinatorial Hodge theory à la Rota conjecture I proved with June and Eric, or positivity of Kazhdan-Lustig polynomials established by Elias and Williamson, this is much better. Because while those arguments relied on a known combinatorial trick by McMullen/de Cataldo-Migliorini, this one used an entirely new idea. First, let me state the theorem, without getting too technical:

We proved, given a triangulated sphere \Sigma of dimension d-1, the face ring (in arbitrary characteristic) permits an Artinian reduction and contains a linear element \ell so that

A^k(\Sigma) \xrightarrow{\ell^{d-2k}} A^{d-k}(\Sigma)

is an isomorphism.

Continue reading →

Scalar curvature and angles of polyhedra: test your intuition

Karim AdiprasitoLeave a comment

I was listening to a marvelous talk by Jean-Pierre Bourguignon today, about generalizations and (geo)metric meaning of scalar curvature, and Misha Gromovs thoughts on the subject. Essentially, just like Alexandrov and Gromov and many others gave us metric understanding of sectional curvature, and Sturm and Lott-Villani and many more gave us metric ways of thinking about Ricci curvature, Misha is at it again to do the same with the weakest notion of curvature.

Jean-Pierre Bourguignon (I will take a less formal picture of him tomorrow)
Misha Gromov (this picture seems informal enough)


One of the goals would be to understand polyhedral spaces from the viewpoint of scalar curvature. In this context, Misha asked me to give a reference for the following statement: Given fixed d and any \epsilon>0, there is a finite number of combinatorially distinct d-polytopes all whose dihedral angles are all smaller than \pi-\epsilon. I will write more about this and scalar curvature later, but for now I am stealing a format from Gil’s blog and ask: Did I have a chance to find such a reference, or do you find examples that make such a statement hopeless? And what \epsilon>0 can you choose safely?

While I am at it, let me add another question for your intuition: Can you deform a polytope such that all dihedral angles do not get bigger? What deformations can you find? More on this subject, and some partial answers to the questions above, later.

Called her Jiji

A note on PL handlebodies, the Hausmann trick and some homology spheres

Karim AdiprasitoLeave a comment

There is a surprising lack of intuition for PL manifolds around, which always surprised me. And it turns out you can answer some questions. We stay in the category of PL manifolds throughout. The following question was asked by Gil Kalai to Ed Swartz some 15 years ago. Ed could not answer the question, and popularized here.

Gil

Question (Kalai) Are there different (homeomorphism types of) triangulated closed compact homology (d-1)-spheres $H$ with g_3=0 (for any d)?

Without going too deep into what g_3=0 means, we note quite simply that it is equivalent to saying that H is boundary to a triangulated manifold D that has no interior simplices of dimension d-3.

The answer to this is yes. In fact, there are infinitely many (). For this purpose, we will make the following observation:

Theorem H. Let d \ge 2. Let M be a PL d-manifold. The following are equivalent:

1. M admits a PL handle decomposition into handles of index \le k,

2. M admits a PL triangulation in which all (d-k-1)-simplices are on \partial M.

Continue reading →

Sofia, Lefschetz via shelling and bonk and the holy trinity (kind of) (part 1)

Karim Adiprasito1 Comment

This is born out of an attempt to find equivariant Lefschetz elements, so to have a combinatorial Lefschetz theorem that is a little less generic for some conjectures in geometric topology. Actually this succeeds to give some interesting results, and I will update in a second part. It will take me some days, in the meantime I made this here simple and clear.

Dear X,

so, Covid seems almost over (fingers crossed). I lost three I loved during the time (none of them due to covid, funny enough; two suicides and a heart failure), I had covid twice (fingers crossed for the hat trick) despite three vaccinations. I am in Sofia, at a inaugural conference of the ICMS.

But that’s not what this post is about. This post is about another proof of the g-conjecture. Well, the Lefschetz property for simplicial cycles, really. It is the simplest one yet, but that is not why it is important. It is also the third one (that is essentially different) and combines the ideas of three teams. (I count the original one by me here, and the characteristic two proof by Papadakis and Petrotou; our joint paper is a combination of the ideas from the former and yada yada yada creative counting to make the holy number work out. Deal with it.) If the first is a refined choreography of slashes and parries that is difficult to follow, and the second the equivalent of wooshing around with bloodhound step (using a miraculous formula that comes out of nowhere), then this is the equivalent of bonking the boss with a hammer: we write down a rational function and examine it, observing it has a pole to show it is nontrivial. Unfortunately it seems to be less general than either of the previous proofs, but I will see whether it can be pushed.

Continue reading →