A while ago, Janos Pach told me a question of Peter Maga originating in topological graph theory: Given an arrangement of curves in the plane, can they be realized as geodesics? Due to my Nikolai Mnev‘s universality theorem (and earlier work by Ringel), it is badly impossible to linearize them (stretch them to line segments), even if we assume that any two curves intersect at most once and at that point transversally, that is, if they form a system of pseudo-segments. However, Janos “just” wanted each curve to be a shortest path.

This had been proven if the segments extend to infinity by Herbert Busemann (who, as I found out, was also an accomplished artist) and so Janos asked whether it was true in general; this of course would be much more reasonable than the realization along lines (note that the space of all metric spaces with given geodesics would be a disk, rather than the arbitrarily nasty deformation space that Kolya proved whe have when looking for arrangements of real lines.)

So, now we want each line to be the shortest, no two points along it should have shortcut somewhere else. A reasonable request; having dabbled in city planning (read: I played Cities: Skylines like, twice) I imagine it must be the worst nightmare of every real estate developer if the carefully named street is not actually used because a detour using other streets is shorter. (Edit: Conferred with a friend who does spatial planning for a German metropolis. It is not something that keeps him up at night. As with all of us, it is depression and anxieties that keep us up and night. And the decision to have coffee in the evening.)

Jokes aside, this can have real applications, as knowing which routes are shortest (geometer speak: knowing the geodesics and shortest paths) makes planning a route considerably easier (CS speak: faster to compute).

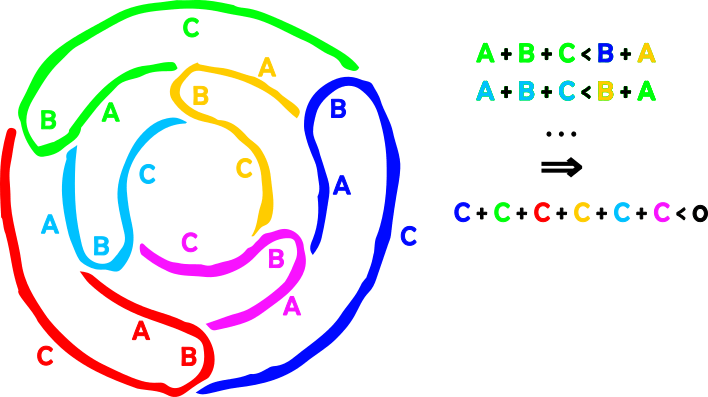
Alas, it turns out to be wrong, and Janos and I found that there are examples where the carefully named and arranged streets are not the shortest. And the aesthetically pleasing example you see here:

It is not hard to see that we cannot give a length metric to this graph such that each of the colored lines is a shortest path; here is the calculation:

Disclaimer: updates to the post were sponsored by an anonymous professor at Rényi Institute